Lean: introduction

Речь пойдет не о Lean Kanban, который все чаще звучит на работе, а о невероятно чудесном языке с зависимыми типами и системе для формальной верификации Lean от Microsoft Research. В текущей серии постов я хочу уложить некоторые вещи в собственной голове, получить простую шпаргалку на русском языке, а также помочь проникнуться системой тем, кому по какой-то неведомой причине влом читать книжку, что тем не менее сделать обязательно нужно (она, воистину, близка к идеалу того, как нужно писать книги подобного рода). Книга проводит читателя через премудрости формальной верификации с помощью системы с зависимыми типами практически под анестезией. Так что, конечно, лучше закрыть этот пост и пойти читать её. Но я же пишу для себя, в конце-концов!

Эта статья пролежала в черновиках больше года. Решив открыть её сегодня, я понял, что на самом деле она готова на 90%. В связи с этим я решил добить всего пару абзацев и, наконец, её опубликовать. А всё самое интересное уже положить в следующие выпуски (с моей скоростью публикаций, видимо, года через два).

Прежде чем разбираться, собственно, с Lean требуется понять, а какую задачку мы решаем, и почему её вообще нужно решать. Для начала введем понятие формальной верификации, упомянутой выше уже дважды. Этим понятием мы будем называть использование логических и вычислительных методов для установления истинности утверждений, выраженных в точных математических формулах. Примером может служить следующее простое выражение, которое мы однажды обязательно докажем формально:

\[ \forall n, m \in \mathbb{N}, n + m = m + n \]

Такие выражения могут содержать не только классические математические теоремы, как пример выше, но и утверждения о корректности программного кода, аппаратных схем, сетевых протоколов, и многого другого. Подобное разнообразие достигается за счет изоморфизма Карри-Говарда, утверждающего, что нет различий между проверкой корректности доказательства теорем и соответствия написанной функции заявленной спецификации, то есть её типу. При этом доказательство, конечно, не дается бесплатно. Во-первых, любую схему, чью корректность требуется верифицировать, требуется формализовать в математических терминах, что может оказаться достаточно нетривиальной задачей. Во-вторых, сама проверка корректности зачастую является вычислительно сложной задачей, затрачивающей значительные аппаратные ресурсы.

Погодите, а зачем это всё?

Ну, во-первых, это красиво. А если серьезно, то основных мотиваций к формальной верификации и автоматическому доказательству (то есть синтезу части доказательства без участия человека) я вижу две.

Первая (фундаментальная) — научить машину мыслить-таки логически и выводить новые знания из имеющихся. Все наши модные нейросетки обладают отличными способностями к обобщению и поиску закономерностей, но ужасны в построении логических заключений на основе данных. Любо-дорого смотреть, как хайповая GPT-3 лажает на простейших вопросах. Так что лишь синтез этих дисциплин однажды сможет привести нас к настоящему сильному искусственному интеллекту.

Вторая (практическая) — быть уверенными, что в доказательствах теорем отсутствуют ошибки. Современные доказательства весьма сложны и занимают сотни страниц (вот, например, 109-страничное доказательство великой теоремы Ферма), а значит проверка их корректности — задача ничуть не более простая, чем оформление самого доказательства. Как мы можем быть уверены в том, что доказательство на 100 листах не содержит ошибки? До сих пор существовал только один метод: дать доказательство на проверку нескольким авторитетным математикам и поверить их заключению. Страшно подумать, математика, царица наук скатилась до веры в авторитеты! Само понятие "верное утверждение" теряет математическую чистоту, поскольку завтра оно может стать уже ложным. И как же теперь презирать все экспериментальные науки? Поручить проверку доказательства машине!

Есть еще товарищи, искренне считающие, что подобные методы позволят выпускать более качественное программное обеспечение, но я в последнее время отношусь к этому довольно скептически. Почему я в это не верю? Несмотря на то, что в этом цикле постов я буду доказывать, как вся эта магия проста и понятна, на самом деле применение таких подходов к разработке программного обеспечения — это очень сложно. Трудозатраты на формальное доказательство значительно превосходят затраты на те же тесты, тогда как разница между 100% и 99% надежностью системы не так критична. Существует исключительно мало областей, в которых готовы переплачивать за этот процент, а потому, эта сфера так и останется маргинальщиной.

Два слова про типы

Рассказывать подробно CoC (Calculus of Constructions) и CiC (Calculus of Inductive Constructions), на котором построены все современные языки с зависимыми типами, которые и используются для доказательств, я не буду. Но какие-то базовые вводные слова сказать стоит.

Типы можно рассматривать как некоторую альтернативу множествам, долгое время игравших роль "базового языка" математики. Другими словами, исходя из простейшей аксиоматики множеств (активно изучаемой в школах и на младших курсах технических ВУЗов) можно придти к произвольным математическим конструкциям от натуральных чисел до многомерных геометрических объектов. К сожалению, несмотря на свою аксиоматическую простоту и описательную мощность, сама теория множеств обладает фундаментальным недостатком: она противоречива, а значит, при желании её инструментарий позволяет доказать что угодно, в том числе очевидно ложные утверждения.

Еще одна широко используемая в школьной математике вещь, от которой стоит отказаться — это неконструктивность доказательств, то есть доказательство какого-то факта не позволяет вам получить доказываемый объект. Например, вы доказываете что существуют два иррациональных числа a и b, такие что \( a^b \) — рациональное. Но при этом не предъявляете сами эти числа. Ну, и зачем нам такое доказательство?

Это привело к появлению двух очень важных для рассматриваемого предмета течений: теория типов и интуиционизм.

Теория типов (точнее, тот вариант, что мы будем здесь рассматривать) устанавливает жесткую иерархию на принадлежность объектов (термов) каким-либо скоплениям — типам. Так, все примитивные объекты будут лежать в тех или иных множествах — типах нулевого порядка, образующих вселенную таких типов Type 0, однако сами множества не могут лежать в других множествах. Вместо этого они будут принадлежать некоторым более крупным структурам — типам первого порядка (Type 1). Аналогично продолжая, мы можем получить правило, что каждый тип порядка u будет лежать в типе порядка u+1, то есть Type u : Type (u+1). Это позволяет избежать парадоксов, внеся еще больше строгости в описание рассматриваемых конструкций. Последним дополнением является кумулятивное вложение вселенных типов друг в друга. Это значит, что любой тип лежит не только в типе уровня на единицу больше, но и во всех типах более высокого порядка.

Под интуиционизмом в самом простом виде мы будем понимать отсутствие аксиомы исключенного третьего (A ∨ ¬A) или, что то же самое, закона снятия двойного отрицания (¬¬A → A). С философской точки зрения это означает, что из опровержения некоторого факта не следует доказательство его отрицания. Другими словами, единственный способ доказать что-то в интуиционизме — привести конструкцию (тот самый конструктивный метод доказательства). Например, для доказательства существования натуральных чисел меньше 10 требуется предъявить хоть одно такое число. А для доказательства упоминаемого выше факта коммутативности сложения натуральных чисел требуется показать, способ приведения обеих частей к одинаковому результату. Далее мы активно будем пользоваться этим соображением, предъявляя конкретные примеры термов, имеющих типы, содержащие утверждения, которые мы хотим доказать.

Setup

Скачать Lean 3 можно с GitHub или в репозиториях вашей операционной системы операционных систем. Пока этот текст готовился, ветка 3.х была заморожена (но продолжается в виде community ветки), сейчас в активной разработке версия 4, но она пока крайне недружелюбна к пользователям.

Для полноценного использования языка нам потребуется совместимая IDE, к которым в настоящий момент относятся Emacs, VIM и VS Code. Я пользуюсь последней, где вся работа выглядит вот так:

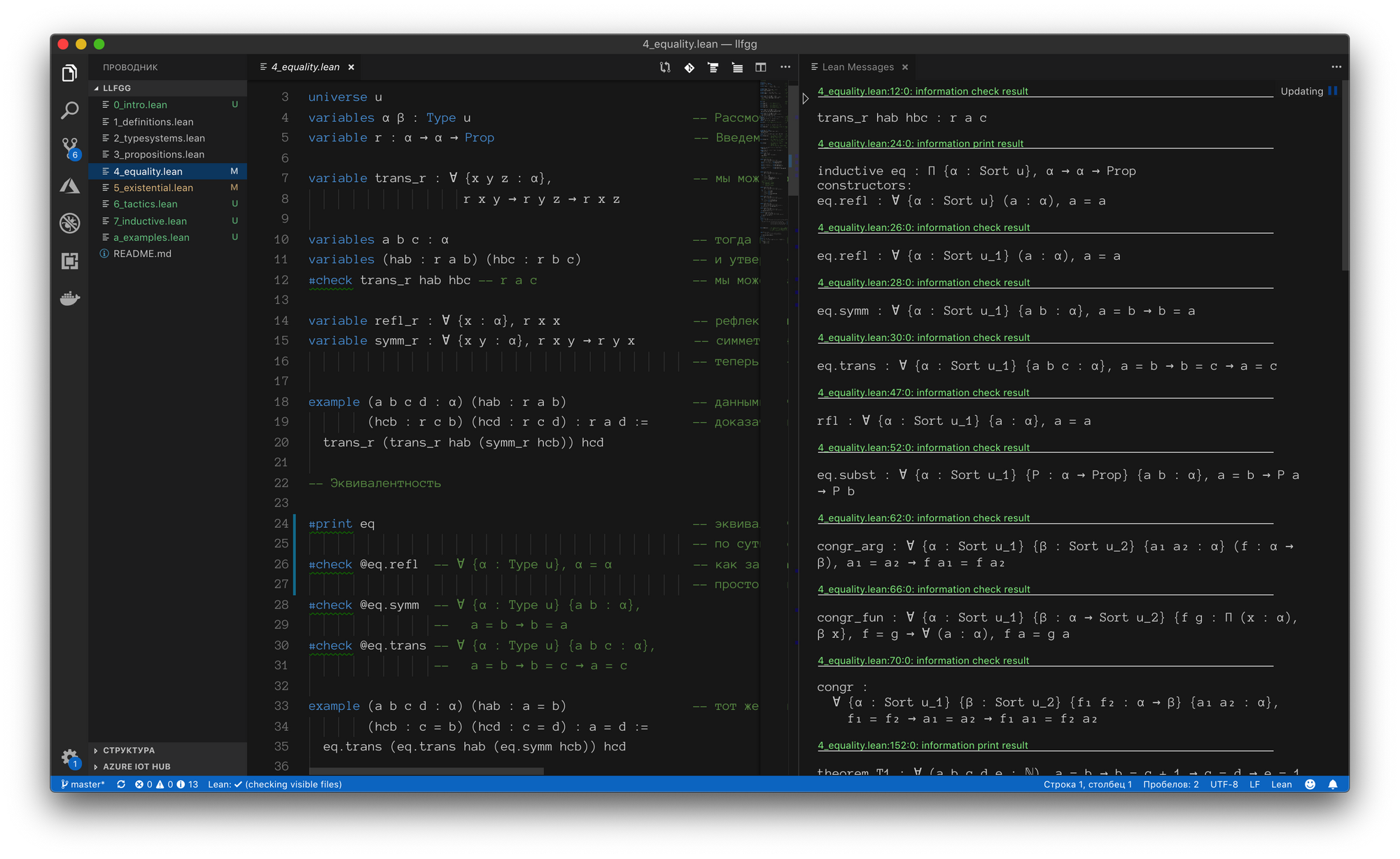
В языке активно применяется юникод, писать который можно и самому. Так, для получения красивого символа ℕ достаточно в VS Code ввести \nat, а красивая лямбда (λ) будет задаваться через \fun или \lam. Главным недостатком использования Lean в VIM, пожалуй, является отсутствие нормальной поддержки этой фишки. В остальном работать не менее удобно:

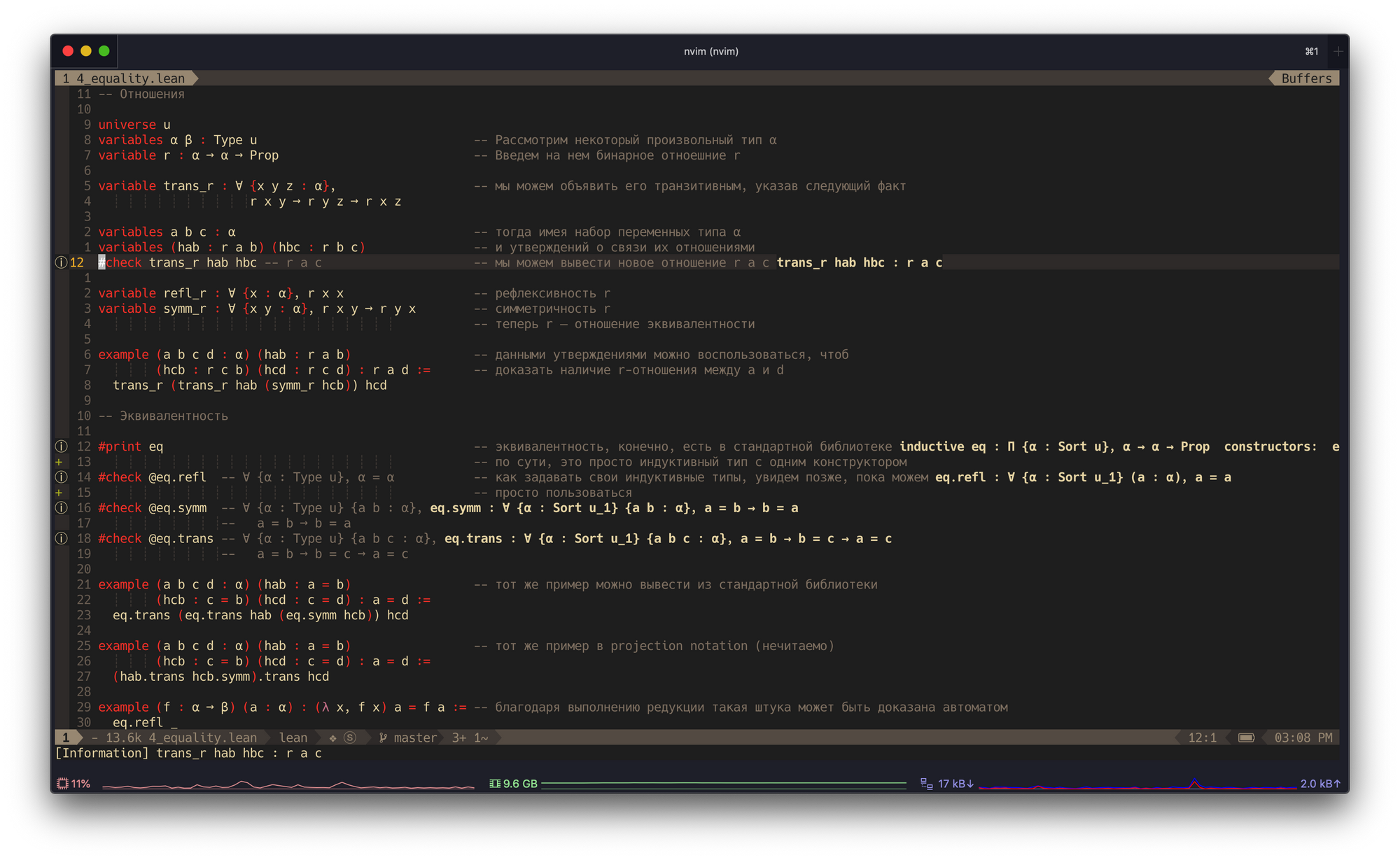
Hello World

Lean — язык, разработанный в первую очередь для формальной верификации, а не программирования в привычном понимании слова. Тем не менее мы можем легко вывести любую строку на экран с помощью команды #print. Для этого мы можем создать простейший файл (скажем, hello_world.lean):

#print "Hello World!"

И запустить его из консоли следующим образом:

$ lean hello_world.lean
Hello, World!

Далее мы не будем пользоваться консольным запуском, предпочитая вместо этого работу в интерактивной среде. Однако писать на Lean можно хоть в Блокноте: все команды, начинающиеся с # будут выводить информацию в stdout при запуске на них интерпретатора Lean.

Вывод типа

Базовой командой, которой мы постоянно будем пользоваться, является команда #check, осуществляющая проверку типа некоторого выражения. Вот несколько примеров её использования:

#check 5
#check 'a'
#check tt

Каждая из этих строчек в процессе выполнения вернет тип выражения. Ими станут:

5   : ℕ
'a' : char
tt  : bool

В Lean объектами первого класса являются не только примитивные значения, но и функции, и типы. Они могут быть использованы как аргументы и значения функций, а значит тоже должны иметь какой-то тип:

#check ℕ
#check fun x, x + 1

Вернет, соответственно:

ℕ                : Type
λ (x : ℕ), x + 1 : ℕ → ℕ

Стрелочная конструкция также может быть протипизирована (для рисования красивой стрелочки требуется воспользоваться сокращением \r):

#check ℕ → ℕ

Такая конструкция, ожидаемо, вновь вернет Type.

Сама конструкция Type может быть протипизирована, ведь это некоторый тип, а типы в Lean, как мы уже сказали, являются объектами первого класса.

#check Type

Поскольку Lean является языком исчисления предикативных индуктивных конструкций, то все типы образуют в нем кумулятивную иерархию. Тип Type (0) лежит в Type 1 и всех более высоких вселенных (Type n). Наш запрос отобразит нам ближайшую:

Type : Type 1

В стандартной библиотеке также определены полезные в натуральном хозяйстве типы суммы и произведения. Называются они соответствующе, а также имеют красивые юникодные обозначения:

#check prod ℕ ℕ
#check ℕ × ℕ
#check (1, 1)          -- будет иметь тип ℕ × ℕ

#check sum nat bool
#check nat ⊕ bool

Вычисление и редукция

Как и в любом нормальном языке программирования мы можем попросить Lean вычислить значение некоторого выражения. Для этого используется команда #eval:

#eval 1 + 2                                 -- 3
#eval (λ x, x + 39) 3                       -- 42
#eval tt && ff                              -- ff

Не все вычисления, однако, заканчиваются каким-то результатом — значением, представимом в виде элементарного машинного типа. В связи с этим более распространенной конструкцией является команда #reduce, приводящая результат в виде нормальной формы:

#reduce (λ x y, x) 1                        -- λ (y : ?M_1), 1

Вывод в данном случае заодно показал нам, как можно специфицировать тип в лямбда-абстракции (использовать стиль Чёрча). Можно воспользоваться этим в следующем примере:

#reduce (λ (x : ℕ) (y : ℕ), x + 10) 1 4     -- 11

В принципе, командой #reduce вместо #eval можно пользоваться всегда. Последняя имеет лучшую производительность, но пока мы не применяем Lean для программирования общего назначения, это не так важно, как удобство однообразия.

Функции

Разумеется, писать на одних лишь только лямбдах было бы весьма неудобно, а потому в Lean есть механизм связывания имен с различными термами. Например, так мы можем задать константную (нулярную) функцию foo, возвращающую натуральное число 5:

def foo : ℕ := 5

Более нетривиальным примером является связывание имени с каким-нибудь типом, который в Lean ничем не отличается от любого другого терма:

def my_bool : Type := bool

От константных функций пора переходить к более интересным, то есть имеющим параметры. Задавать такие функции можно несколькими способами, все они будут эквивалентны и зависят от привычки и чувства прекрасного пользователя. Это обеспечивается благодаря тому, что все функции в Lean по умолчанию каррированы, как в Haskell.

def add1 (n : ℕ) (m : ℕ) : ℕ :=
    n + m

def add2 (n m : ℕ) : ℕ :=
    n + m

def add3 (n : ℕ) : ℕ → ℕ :=
    λ m, n + m

def add4 : ℕ → ℕ → ℕ :=
    λ n m, n + m

Поддержка зависимых типов позволяет в типе возвращаемого значения использовать аргументы. Это значит, что в стрелке A → B тип B зависит от значения a, иными словами, a как-то участвует в записи B. Такую конструкцию принято записывать в виде Π (a : A), B. Приведенная же выше стрелка является синтаксическим сахаром для частного случая, когда B от a не зависит. Тем не менее можно написать полную дешугаризированную версию:

def add5 : Π (n : ℕ), Π (m : ℕ), ℕ :=
    λ n m, n + m

Разумеется, как любой приличный язык, Lean поддерживает довольно-таки продвинутый pattern matching аргументов, что позволяет объединить все имеющиеся у нас знания и применить их для получения чего-нибудь очень практически полезного. Например, функции вычисления чисел Фибоначчи:

def fib : ℕ → ℕ
| 0 := 1
| 1 := 1
| (n + 2) := fib n + fib (n + 1)

Ну, всё, можно программировать! Но собрались мы тут, конечно не для этого. Так что в следующий раз введем несколько необычных для привычных языков программирования конструкций, посмотрим на реализацию разных систем типов и, наконец, окунемся в теоремы.